Problem: A portion of an amusement park ride is shown. Find EF. Justify your answer.

You may have guessed that this is a similar-triangles problem and you would be correct! Just from looking at this diagram, it appears that ▲ADE is similar to ▲CBE, so we can start by proving this.
First we can state that BD || AD (both vertical pillars are parallel) since they are perpendicular to the ground. Then, we must prove that at least two angles are the same. By the alternate interior angles theorem, we can conclude that ⦟ADE = ⦟CBE and that ⦟DAE = ⦟BCE
Since all of the interior angles in a triangle add to 180°, and we have proven that two angles are the same, we can now state that the third angle is equivalent. This makes sense since the remaining angles are opposite angles and are equal by this property as well. Since all three angles are the same, we can simply state that ▲ADE ~ ▲CBE
Next, let’s draw a diagram so that the length EF can be solved for.
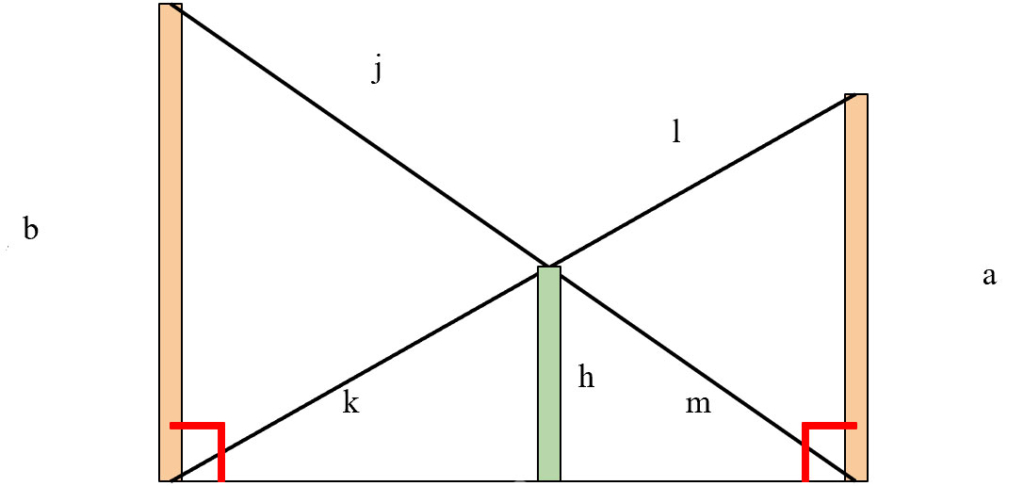
Here, we assign variable names to each edge and rename EF to h.
Because the two triangles that we created are similar, we can say that

We need to do one more step so that we can write a similar triangle relationship that includes h.
If we subdivide the similar triangles like this
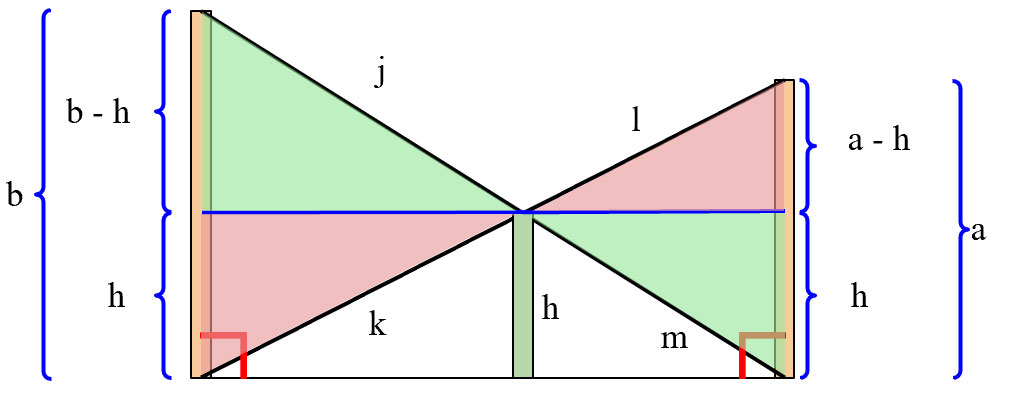
We now have new similar triangles in red and green to write relations for in terms of h, a, and b.
Now that we have the red and green similar triangles, we can write expressions to relate them and solve for h.
Let’s start with the green triangles. Since they are similar, we can say that
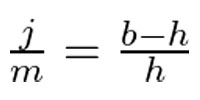
Likewise, we can say about the red triangles that
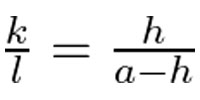
Using the relation from the original two triangles

The two new relations can be substituted in:

Now we can solve for h.
Cross multiply:
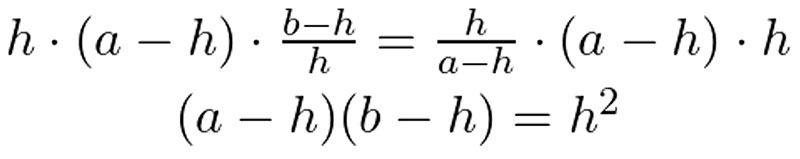
Distribute:

Subtract:
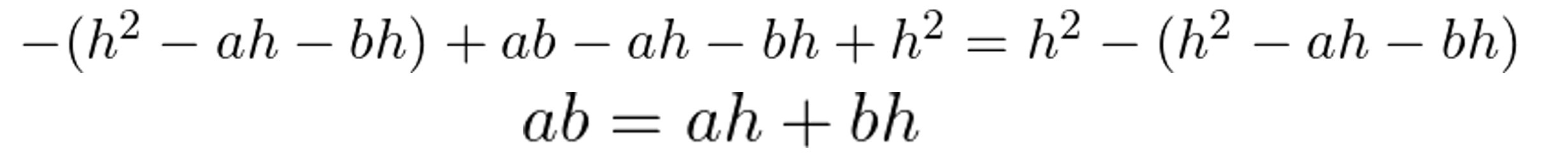
Factor:
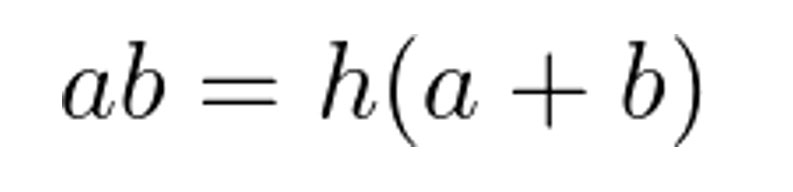
And finally, divide:
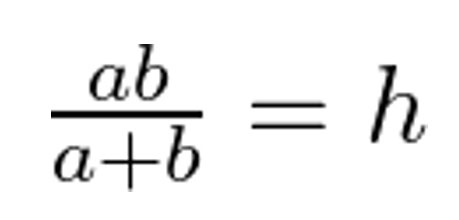
Now that we have a solution, we can plug this in the original heights of the columns a and b.
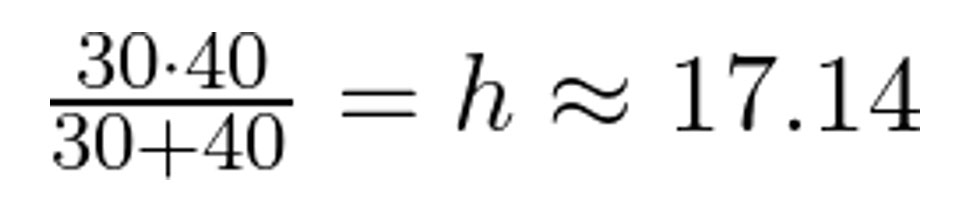
So the height EF is approximately 17.14 feet.
